

|
| Home | Институт | Администрация | Лаборатории | Объявления | Сотрудники | Cсылки | O нас |
|
| Разломная Тектоника Материковой Части Дальнего Востока России (Глава 2) | |||||||||||||||||||||||||||||||||||
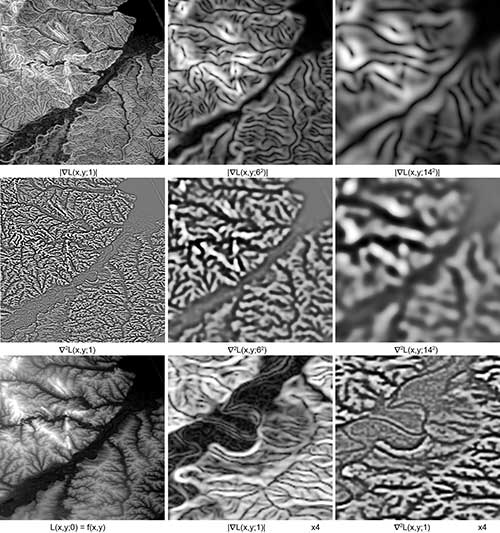
Рис. 2.5.1. Кольцевые образования на р. Тымь, (о. Сахалин, пос. Ноглики, координаты 51°40' с.ш. и 143° в.д.), размер каждого изображения примерно 40х40км (верхний ряд) модуль градиента масштабных представлений, когда параметр t = 1, 36 и 196 (средний ряд) оператор Лапласа того же набора (нижний ряд, левый) ЦМР, т.е. исходные данные f(x,y), преобразованные для визуального восприятия (нижний ряд, центральный и правый) увеличенные в четыре раза (х4) центральные участки изображений модуля градиента и оператора Лапласа масштабных представлений с параметром t=1. LQ (500x500 pix). HQ (1500x1600 pix, 284KB). 
Рис. 2.5.3.1 В формировании изображения принимали участие несглаженная модель высот (канал R), "модуль градиента" при t=1 и "оператор Лапласа", t=1. Т.к. каждый канал представлен наиболее подробными компонентами, такую схему удобно использовать в ситуациях, когда требуется максимальная деталировка элементов рельефа. HQ (500x500 pix, 146KB). 
Рис. 2.5.3.2 Канал R - "оператор Лапласа", t=36. Канал G - "модуль градиента", t=1. Канал B - "оператор Лапласа", t=1. HQ (500x500 pix, 155KB). 
Рис. 2.5.4. Пример цветного синтезированного изображения. Район Центрально-Сихотэ-Алиньского разлома на Дальнем Востоке России. Составляющие RGB изображения: R – исходный рельеф; G и B –модуль градиента рельефа с масштабными параметрами t=1 и 62 соответственно. LQ (500x500 pix, 112KB). MQ (2000x2000 pix, 1.7MB). HQ (6519x5478 pix, 12MB). 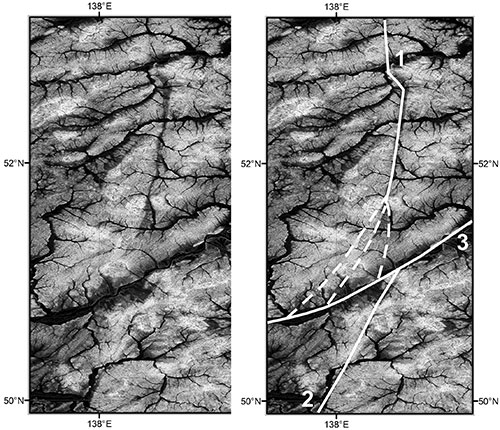
Рис. 2.6.1. Пример линейной структуры. Лимурчанский разлом на Севере Сихотэ-Алинской складчатой системы, Дальний Восток России. Белыми сплошными линиями показаны: 1- Лимурчанский разлом; 2-Центральный Сихотэ-Алиньский разлом; 3-Киселевский разлом. Пунктиром показано возможное продолжение Лимурчанского разлома. LQ (500x430 pix). HQ (2215x1903 pix, 1.3MB). 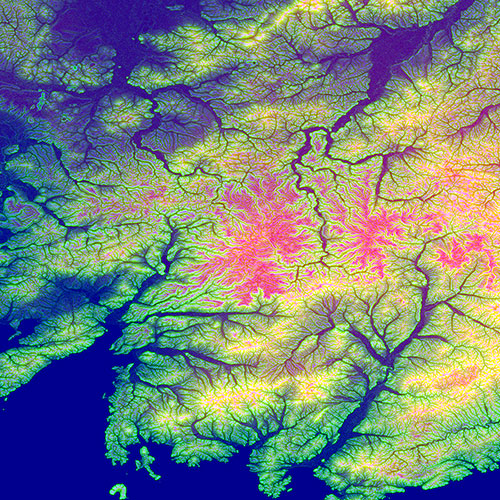
Рис. 2.6.2.1. Потоки базальтов на Шкотовском плато на юге Приморья, Дальний Восток России. Координаты 43°40' с.ш. и 133° в.д.. Изображение является синтезом RGB каналов состоящим из компонентов: ЦМР, t=0, G – "модуль градиента", t=1, Канал B - "оператор Лапласа", t=1. LQ (500x500 pix, 191KB). HQ (2000x2000 pix, 2.3MB). 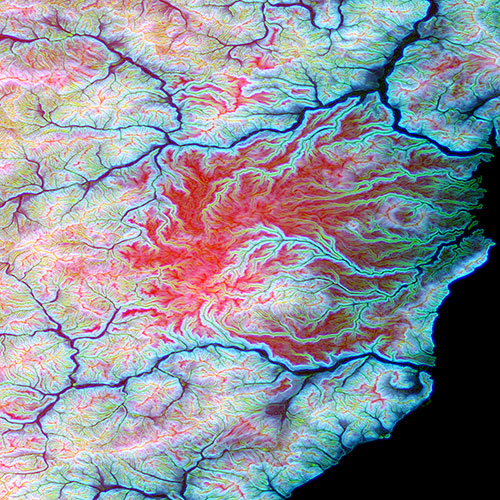
Рис. 2.6.2.2. Район г. Совгавань на границе Хабаровского и Приморского краев, Дальний Восток России. Координаты 49° с.ш. и 140° в.д.. Изображение повторяет предыдущую схему за исключением того, что синий цветовой канал B – "модуль градиента", t=36. LQ (500x500 pix, 159KB). HQ (2000x2000 pix, 1.4MB). 
Рис. 2.6.3. Пример выделения кольцевой структуры в Восточно-Сихоте-Алинском вулкано-плутоническом поясе. Синтезированное RGB изображение, где составляющие RGB получены путем расчета Лапласиана поверхности Гаусса с масштабными параметрами t=62,1,142 LQ (500x500 pix, 142KB). HQ (1448x1448 pix, 1.4MB). |
О.В.Рыбас, Г.З. Гильманова,
Институт тектоники и геофизики им. Ю. А. Косыгина ДВО РАН, Хабаровск 2014 o_rybas @ itig.as.khb.ru gigulya @ yandex.ru При исследовании сложных сигнальных последовательностей часто возникает задача, связанная с выделением их структур, т.е. частотных характеристик, инвариантов, связей между ними. Но если в пределах одной и той же технологии выделения структур использовать некую сигнальную последовательность с различными уровнями деталировки, результаты на выходе могут отличаться. То есть, к примеру, больше деталей в сигнале обеспечит более выраженное присутствие высокочастотной компоненты в выделенной структуре по сравнению с огрубленной сигнальной последовательностью, где, соответственно, будут доминировать низкочастотные составляющие. Когда отличия существенные, возникает возможность использовать их как взаимодополняющие конструкции, позволяющие строить максимально полную картину о характере исследуемого сигнала. Введем термин "масштаб", не в классическом понимании этого слова как отношение единиц измерения карты к единицам измерения пространства, а как величину, характеризующую деталировку сигнальной последовательности, т.е. масштаб следует понимать в контексте точности представленной информации. В литературе иногда используется термин "внутренний масштаб", который можно оценивать как количество деталей (локальных экстремумов) на единицу объема, тогда минимально возможное расстояние между ними будет соответствовать квадратному корню некой величине t, которая имеет собственное название: "параметр масштаба". Следовательно, исследуемый n-мерный сигнал рассматривается в расширенном пространстве размерности n+1, где параметр масштаба занимает дополнительное измерение. Такое "расширенное" пространство определяется как масштабное. Возникает вопрос, каким образом исходную информацию можно преобразовать так, что бы деталировка при огрублении (увеличении масштаба) монотонно уменьшалась, не создавая при этом новых особенностей. Наиболее очевидным и естественным было воспользоваться физическим процессом диффузии, когда концентрации вещества в некий момент времени t ставится в соответствие величина исследуемого сигнала L в масштабном пространстве с параметром масштаба t. По этой причине время в уравнении диффузии (теплопроводности) и масштаб в нашей теории обозначается одним знаком. Сделаем небольшой экскурс в историю. В 1983 г. Эндрю Виткиным (Witkin, 1983) был предложен метод обработки 1-мерных сигнальных последовательностей сверткой с ядром Гаусса и введен термин "масштабное пространство" ("Scale-space"), и год спустя Кендеринк (Koenderink, 1984) показал справедливость этого метода для 2-мерного случая, в частности, для обработки растровых изображений. Следующим шагом было определение оператора "ядра производной Гаусса" ("Gaussian derivative kernel") и мультимасштабного представления, основанное на гауссовых производных, которое было предложено Кендоринком и ван Доорн (Koenderink and van Doorn (1987)) в качестве возможной модели для первичной обработки видеоинформации, т.е. описания механизма зрения, как для биологических объектов, так и для искусственных. Ради справедливости следовало бы отметить, что первая работа на эту тему появилась в Японии в 1962 г. (T.Iijima, 1962), но, т.к. у статьи не было перевода на какой-либо из европейских языков, "западным" исследователям она была недоступна. Таким образом, теория масштабных пространств явилась результатом исследований применения диффузии к n-мерным сигнальным последовательностям (в частности, к любым 2-мерным изображениям), где формально доказаны очень важные и уникальные свойства решений уравнения диффузии. В частности, между элементами масштабного пространства (назовем их масштабными представлениями исходной n-мерной сигнальной последовательности масштаба t) выполняются следующие условия: минимальные расстояния между особыми точками будут находиться в прямой зависимости от величины масштабного параметра и при его увеличении деталировка будет монотонно уменьшаться, не создавая новых особенностей - т.е. локальные экстремумы могут блуждать друг относительно друга и в конечном итоге взаимно уничтожаться (аннигилировать), но никогда не будут порождены новые. Это свойство гарантирует отсутствие ложных структур при исследовании сигнальных последовательностей. Сегодня теория масштабных пространств является одной из базовых для построения более широкой теории компьютерного зрения, а благодаря своей проработанности и простоте реализации она находит применение и в смежных областях знания. В частности, в настоящей работе рассматривается методика выделения структур рельефа по данным их цифровых моделей.
Под цифровой моделью рельефа принято понимать 3-х мерный объект на регулярной 2-х мерной сетке, где каждой ячейке с координатами (x,y) ставится в соответствие величина f(x,y) - высота (чаще всего в метрах). Если существует географическая привязка, то каждая точка (x,y) имеет реальные географические координаты в единицах измерения привязки и, соответственно, расстояние между центрами соседних ячеек (пикселей) принято называть пространственным разрешением в географических единицах измерения. Строго говоря, ЦМР без привязки не имеет смысла, т.к. ее единственная задача - поставить в соответствие набор точек со своими координатами их среднему значению высот в пределах пространственного разрешения. И это идеальный случай. В реальности же получить точную и чистую модель очень дорого, т.к. необходимо не только не допустить выход за пределы погрешности по горизонтальным и вертикальным компонентам, но и шумов в виде неестественных локальных выбросов (такое происходит из-за неаккуратной съемки или обработки исходного материала). Следует отметить, что цифровые модели могут строиться и на нерегулярной сети, это векторная форма записи ЦМР, где каждый узел характеризуется 3-х мерными координатами (x,y,z) и имеет собственное название «triangulated irregular network» (TIN). Существуют процедуры конвертирования, основанные чаще всего на различных видах интерполяции между растровой моделью на регулярной сети и векторной TIN на нерегулярной. Так как предметом нашего исследования является растровая модель, не будем углубляться в подробности TIN. Даже если цифровая модель построена и удовлетворяет всем требованиям по точности и зашумленности, следует различать два типа моделей: рельефа и поверхности. Если ЦМР – это набор высот поверхности (грунта) планеты над уровнем моря, то "цифровая модель поверхности" - это максимальные отметки высот всего, что на поверхности находится (растительность, искусственные строения). Каждая модель лучше или хуже выполняет разного рода задачи, разумеется, для геологических задач наиболее подходящей должна быть модель рельефа без каких-либо дополнений. Рассмотрим подробнее, чем являются исходные материалы и как строятся ЦМР. Рабочим материалом для исследований и обработки служила цифровая модель рельефа SRTM03, которая построена по радиолокационным снимкам Shuttle Radar Topography Mission (SRTM), и Aster GDEM (Global Digital Elevation Model) на базе стереопар Aster. Распространяемые данные SRTM03 имеют следующие характеристики: размер ячейки 3"х3" арксекунды на пиксель, что соответствует примерно 90 м/пиксель на экваторе и 60-70 м/пиксель для средних широт; проекция Lat/Lon на эллипсоиде WGS84 (World Geodetic System 1984) с исходной отметкой над уровнем моря, определяемой геоидом WGS84-EGM96 (Earth Gravitational Model). Абсолютные погрешности горизонтального позиционирования и высоты для Евразийского континента составляют 8.8 м и 6.2 м, соответственно. Данные кодируются 16 битами, что позволяет представлять весь набор высот от 0 до 65535 м с дискретностью 1 м. Съемка SRTM велась в пределах 56° ю.ш. и 60° с.ш.. Aster GDEM обладает почти теми же характеристиками, за исключением размера ячейки и точности. Ячейка – 1"х1" арксекунды на пиксель, примерно 30 м/пиксель на экваторе и 20 м/пиксель для средних широт. С точностью до 17 м по вертикали попадает 95% отметок высот при пространственном разрешении по горизонтальным компонентам 75 м. В отличие от радиолокационной съемки SRTM, где его ЦМР является моделью высот грунта над уровнем моря, Aster GDEM – это модель поверхности максимальных высот (не модель рельефа в дословном понимании этого слова), т.к. она строилась по стереопарам оптического диапазона. Соответственно, все города, трубы, дороги, просеки в лесах присутствуют в этой модели, что может мешать в интерпретации результатов анализа. Но это может оказывать влияние только при исследованиях с очень высоким уровнем деталировки, все-таки линейные размеры различного рода дислокаций и искусственных или биологических образований несопоставимы, и эта проблема теряется на фоне другой - зашумленности. Для ослабления уровня шумов до приемлемого уровня, необходимы дополнительные процедуры очистки и огрубления до трех арксекунд на пиксель пространственного разрешения (60-90 м в ячейке). После этого детализация становится сопоставимой с ЦМР SRTM03, а точность хуже, и не все шумы удается удалить. Тем не менее, Aster GDEM может быть полезен для исследования приполярных областей, т.к. его зона покрытия +/- 83°. Отдельно хочется отметить, что выборочные исследования подробных ЦМР с пространственным разрешением 20-30 метров на пиксель показали неудовлетворительные результаты по сравнению с более грубыми моделями рельефа. Это объясняется не только растительным покровом (если речь идет о стереопарах), но и слишком высокой деталировкой приповерхностных деформаций рельефа, которые создают слишком много шумов, от которых можно избавиться только методом огрубления. Учитывая тот факт, что поиск минимально возможных дислокаций - это поиск объектов с линейными размерами не менее километра, тогда можно сделать оценку, что 90 м в пикселе ЦМР является почти идеальным пространственным разрешением для этой задачи.
Прежде всего, введем несколько определений. Необходимо оговориться, что все дальнейшие положения справедливы для пространств любой конечной размерности, но в нашем случае задача сводится к выявлению структурных особенностей рельефа - поверхности, где каждой точке с координатами (x,y) поставлена в соответствие ее высота f(x,y). Для любого непрерывно дифференцируемого и интегрируемого отображения
где ⊗ - оператор свертки,
и t - параметр масштаба. То-есть, результат свертки L(x,y;t) - это масштабное представление поверхности f(x,y) с коэффициентом масштаба t. Иногда говорят: слой (Layer) в масштабном пространстве параметра t. При t=0 ядро свертки превращается в импульсную функцию и f(·)=g(·;0)⊗f(·), т.е. поверхность остается неизменной в результате такой операции. Множество L(x,y;t) является одним из решений линейного уравнения диффузии (теплопроводности), где роль параметра времени t в нашем случае играет параметр масштаба
с начальным условием L(x,y;0)=f(x,y). Это одно из широко используемых и хорошо исследованных дифференциальных уравнений в физике, что позволяет нам наглядно представлять процесс сглаживания сигнала (диффузию компонентов) по отношению к масштабу (времени), и аналитически описывать и просчитывать характеристики обрабатываемого сигнала. Заметим, что в результате операции свертки двух элементов, когда оба являются ядрами Гаусса, сформируется третий элемент, который также будет ядром Гаусса и будет принадлежать исходному множеству: g(·;t1+t2) = g(·;t1) ⊗ g(·;t2) , t1, t2 > 0 Тогда можно видеть, что множество гауссовых ядер
и для любого масштабного представления справедливо следующее равенство:
Следовательно, каждый элемент масштабного представления L(x,y;t2) можно получить как сверткой ядра g(x,y;t2-t1) по отношению к предыдущему преобразованию L(x,y;t1), так и прямой сверткой g(x,y;t2) по отношению к функции f(x,y). Это дает свободу выбора при построении фильтров различных масштабов и позволяет контролировать величину масштаба конечного результата в ходе последовательных (комплексных) преобразований. Следует обратить внимание на то, что масштабная компонента t не может принимать отрицательных значений и, следовательно, не существует обратных элементов, которые превратили бы исследуемый объект в группу. Этот факт является формальным подтверждением того, что не существует преобразований, которые в грубом исходном материале могли бы "найти" тонкие структуры. Одно из свойств явления диффузии – необратимость процесса, и это одно из важнейших свойств гауссовых сглаживаний. Более того, ядра свертки, построенные на базе функций Гаусса, являются единственными, обладающими такими свойствами (Florack et al., 1992). Геометрический смысл свертки поверхности f(x,y) с ядром Гаусса – это сглаживание поверхности с определенным параметром масштаба t. При этом величина t связана с результатом операции L(x,y;t) таким образом, что из исходного изображения удаляются все детали, линейные размеры которых не превышают величину В качестве иллюстрации рассмотрим сигнальную последовательность f(x) построенную как произведение двух зашумленных гармонических функций. Тогда L(x;t) - это ее набор масштабных представлений, с начальным условием f(x) = L(x;0). На рис.2.2.1 (верх), a показано сглаживание формы графика при изменении параметра масштаба t. Зависимость расположений точек перегиба L(x;t) (горизонтальная ось x) от масштаба (вертикальная ось t) представлена на нижней части рис.2.2.1. На этом изображении показаны абсолютные значения второй производной относительно параметра t с последующей обработкой для визуализации треков миграции точек перегиба и минимумов-максимумов. Точка перегиба находящаяся на склоне графика характеризуется условием Lxx = 0 и Lxxx ≠ 0, где индексы означают вторую и третью производную, соответственно. Тогда каждый трек такой точки можно рассматривать как некий объект (полудугу) показывающий ее пространственную миграцию в зависимости от величины сглаживания t. Так как обрабатываемая функция (сигнальная последовательность) непрерывно дифференцируема на всей области определения, то для каждой точки перегиба может быть найдена другая сопряженная с ней относительно соседнего внутреннего локального экстремума (минимума или максимума) точка, которая так же будет мигрировать. При достижении масштаба t некоторого критического значения их треки (полудуги) соединятся и прекратят свое существование (аннигилируют), в этой точке Lxxx(x;t) = 0. Следует обратить внимание, что дуги сформированные парой точек перегиба могут быть закрыты (существует точка, где касательная параллельна оси x) сверху, но всегда открыты снизу, т.е. невозможна ситуация, когда найдется точка, которая в состоянии породить новый экстремум при увеличении t. Этот пример позволяет нам наглядно представить процесс сглаживания с точки зрения миграции особых точек и демонстрации вышеизложенного тезиса о неспособности порождения новых (ложных) структур. В работе 1984 года "The structure of images " Koenderink показал эти же свойства для двухмерных объектов (изображений).
Для любого фиксированного значения t существуют частные производные, которые также обладают свойствами ассоциативности и коммутативности
Масштабные представления, основанные на сглаженных производных (Гауссовых производных), были предложены в работе (Koenderink,1984, Koenderink et al., 1987). На рис.2.3.1 показаны некоторые наиболее часто используемые. Частная производная по каждой из пространственных переменных для поверхности рельефа Lx и Ly - это характеристика изменения высот по соответствующим направлениям. Вектор (Lx, Ly)T – это градиент функции L(x,y;t), который указывает направление наискорейшего роста функции в каждой точке (x,y) и модуль, которого равен скорости ее изменения в этом направлении. Таким образом, градиент характеризует состояние поверхности, как по крутизне, так и по направлению склона (азимуту). Модуль градиента и его азимут вычисляются по формулам
2.4. Мультимасштабные представления
Мультимасштабное представление определяется как набор представлений L(x,y;t) и их производных на базе масштабного параметра t. Необходимость его использования обусловлена тем, что для объектов реального мира не существует такого универсального масштаба, когда можно было бы выделить все элементы структуры в течение единственной серии преобразований. Чаще всего тонкие особенности лучше проявляются при малых значениях сглаживающего параметра масштаба t, при этом теряются в деталях грубые элементы. При увеличении t происходит генерализация обрабатываемой поверхности f(x,y) с потерей детальности, но появляется возможность проявить более крупные региональные структурные составляющие. Таким образом, при проведении серии обработок поверхности f(x,y) (это может быть модуль градиента, лапласиан на поверхности Гаусса, любое другое преобразование) с различной степенью генерализации может быть получена серия результатов, которая, в свою очередь, может быть использована для дальнейшей обработки в аналитических системах (линеаменты, текстуры и др.). Например, выделяя линеаменты из модуля градиента фиксированного параметра сглаживания t, мы всегда можем знать характеристики необходимых на данном этапе обработки объектов и отфильтровывать ненужные (рис.2.4.1). Проделав эти операции для каждого из уровней генерализации, на последнем шаге можно объединить все выделенные линеаменты для получения общей картины.
Рассмотрим модель поверхности рельефа как трехмерный объект в системе координат растрового изображения (x,y), не географического, хотя значения в каждой точке f(x,y) удобней оставлять без изменений, т.е. равными численным значениям реальных высот поверхности над уровнем моря в единицах измерения модели. Так как исходное изображение имеет полную информацию о привязке и системе координат, на этапе обработки нет необходимости в отслеживании географической информации, она вернется на финальном шаге для дальнейшей работы в ГИС-приложениях. Другими словами, ЦМР на этапе преобразований в рамках теории масштабных пространств рассматривается как растр, где гауссовы производные и операторы сглаживания выполняют роль фильтров. Рельеф (как растр) обладает некоторыми характерными свойствами, в частности, полным отсутствием правильных геометрических объектов (линии, окружности и т.д.) - если они есть, это ошибка, и в дальнейшем такие участки удаляются. С другой стороны, линейные и кольцевые структуры рельефа, ради выделения которых проделана наша работа, часто являют собой едва заметные образования, и конечная цель использования теории масштабных пространств – поиск таких масштабных представлений, их производных и комбинаций, когда максимально ярко выделяется какой-либо из видов дислокаций.
Линейные объекты. Модуль градиента является наиболее эффективным инструментом для выделения линейных структур, в зонах разрывных нарушений почти всегда присутствуют пространственно вытянутые участки с близкими значениями градиентов. Кроме того, в любой точке экстремума значение модуля градиента близко к нулю, что позволяет отчетливо выделять долины и хребты. В результате обработки с участием частных производных первого порядка получается изображение, готовое для дальнейшей обработки средствами линеаментного и текстурного анализа. Азимут также может быть использован в качестве дополнительного параметра.
Объекты куполообразной формы. Для выделения объектов куполообразной формы используется оператор Лапласа. Результатом работы фильтра на его основе (иногда его называют "лапласиан поверхности Гаусса (Laplacian-of-a-Gaussian - LOG)") будет максимальная ответная реакция на объекты куполообразной формы (отдельно стоящие пики, горные хребты), очертания которых максимально близко соответствуют форме ядра свертки LOG, и минимальная реакция - на объекты противоположной формы (депрессии, долины). Поэтому поверхность ∇2L=Lxx+Lyy является индикатором пиков/депрессий, линейные размеры которых зависят от масштабного параметра сглаживания t. Фактически, это индикатор пликативных и инъективных нарушений, и на практике это преобразование используется для выделения кольцевых структур и для текстурного анализа. Необходимо сделать замечание, что выделенные линейные и куполообразные объекты на растре не имеют жесткой привязки к методу выделения, речь идет всего лишь о предпочтении одного по отношению к другому в зависимости от типа исследуемой структуры. То-есть, модуль градиента вполне достоверно выделит кольцо какого-нибудь палеовулкана как дугу, построенную по вершинам горных хребтов, также как и преобразования рельефа, выполненные оператором Лапласа, покажут линейные объекты как вытянутые в цепь серии пиков или депрессий. Разница будет только в выраженности типа структуры в зависимости от способа ее получения. Хотя бывают исключения - ситуации, когда модуль градиента ЦМР более нагляден при визуализации кольцевых объектов, чем оператор Лапласа; обратное тоже верно. В качестве иллюстрации существует очень интересный с разных точек зрения объект - это три (четыре) пересекающиеся кольцевые структуры (рис.2.5.1). Место расположения – р. Тымь на Сахалине в 20 км от ее впадения в Ныйский залив (гавань Анучина) и 10 км выше по течению пос. Ноглики; координаты 51°40' с.ш. и 143° в.д. Объект интересен как минимум по двум причинам. Первая, кольцевые образования модуль градиента выделил отчетливее, чем оператор Лапласа (такое редко бывает). Вторая, при масштабе t=1 отчетливо выделены два маленьких соприкасающихся кольца с обрамляющей дугой с юга, при этом более широкая полудуга с юго-востока почти не проявляет своего присутствия (теряется на фоне мелких деталей). При масштабе t=36(62) полностью растворяется одно из маленьких колец, от другого остается только едва заметный след, но зато полностью проявляется обрамляющая полудуга на юго-востоке. При t=196(142) модуль градиента ничего не оставляет кроме русла реки Тымь, после оператора Лапласа результат почти тот же, т.к. остаток от полукольца почти не идентифицируется самостоятельно. Фактически, это демонстрация необходимости мультимасштабных преобразований. И еще этот пример говорит о том, что при поиске структур рельефа необходимо использовать все виды операторов и все доступные масштабные параметры (в разумных пределах) независимо от того, какой тип структуры ищется. Особым объектом исследований являются текстурные особенности рельефа, которые проявляются во всех видах преобразований. Зоны с ярко выраженными морфометрическими признаками (осадочные бассейны, горные массивы и т.д.) можно рассматривать в качестве индикатора состава пород и крупных литолого-петрографических комплексов. Текстуры так же можно использовать как для визуальной оценки, так и в качестве исходного материала для текстурного анализа.
Синтезированные цветные изображения. Для визуальной оценки полученных результатов очень наглядный результат дает сборка масштабных представлений и их производных различных порядков в синтезированные RGB-изображения. Например, цветная картинка из трех масштабных представлений модуля градиента с разными масштабными параметрами позволит показать одновременно и высокочастотные элементы рельефа из представлений с низкими значениями масштаба, и грубые низкочастотные. Если собрать в единое изображение приведенный выше пример с кольцевыми структурами на реке Тымь (рис.2.5.1), где часть из них проявляется только на подробных представлениях, другая – на грубых, можно видеть весь набор дислокаций доступных для минимальных и максимальных значений масштабных параметров (рис.2.5.2.3). Тоже самое можно проделать с представлениями прошедшими через оператор Лапласа (рис.2.5.2.3). Цвет сам по себе ничего не означает, важно его наличие, это говорит о разнице между представлениями с разными масштабами, и чем более выражен цветовой оттенок на определенном участке, тем большая на нем разница в деталировке. Кроме цветовой дифференциации масштабных параметров, достаточно наглядные результаты, с точки зрения вопроса визуализации геоморфологических особенностей, можно получить, собрав в синтезированное изображение представления не только с разными масштабами, но и разными операторами. Вернемся к примеру (рис.2.5.2.1), где оператор "модуль градиента" масштабного представления показывает его крутизну (перепад высот), т.е. более высокому абсолютному значению градиента соответствует крутизна рельефа в соответствующей точке, безотносительно к высоте над уровнем моря. Но если возникает потребность увидеть ее взаимосвязь с текстурными особенностями, можно подставить в один из цветовых каналов RGB-изображения модель высот, предварительно проделав такие преобразования, чтобы ее гистограмма была согласована с соседними каналами. На (рис.2.5.2.2) в канале красного располагаются высоты, в двух других - модули градиента с разными масштабными параметрами. В таких синтезированных изображениях нет смысла использовать сглаженные модели рельефа, т.к. визуально разница почти не видна, поэтому везде, где нет производных, параметр всегда равен нулю (t=0).
На рис.2.5.3.1 и 2.5.3.2 показаны более сложные комбинации, где участвуют и модель высот, и операторы "модуль градиента" и "оператор Лапласа" в различных сочетаниях. Здесь задача сводится к поиску таких комбинаций масштабных представлений и их операторов, когда изображения максимально наглядно выделяют и разделяют геологические или тектонические структуры. Разумеется, эта технология интересна исключительно для визуальной оценки, но учитывая тот факт, что каждое изображение может иметь географическую привязку, бывает очень полезным использовать его в качестве подложки для создания новых или уточнения старых карт. Критерий выбора масштабных параметров для равномерного распределения уровней деталировки при построении серии масштабных представлений. При работе с мультимасштабными представлениями рано или поздно возникает вопрос о том, какой набор масштабных параметров необходимо использовать для наиболее эффективного разделения представлений.
2.6. Примеры применения теории масштабных пространств для решения геологических задач. Ранее вышеописанная методика апробировалась при изучении Алдано-Станового щита (Гильманова Г.З., Рыбас О.В., Горошко М.В, 2011; Гильманова Г.З., Б.Ф. Шевченко, О.В. Рыбас, Е.Ю. Диденко, С.В. Головей , 2012), области сочленения Центрально-Азиатского и Тихоокеанского подвижных поясов (Горошко М.В., Шевченко Б.Ф., Гильманова Г.З. 2013), Учуро-Майской впадины (М.В. Горошко, Г.З. Гильманова, 2013.), Южно-Синегорской впадины (Горошко М.В., Гильманова Г.З., 2012). Рассмотрим несколько примеров применения методики при анализе структур рельефа в различных геологических исследованиях.
1. Линейные элементы - зона сочленения Лимурчанского и Центрального Сихотэ-Алинского разломов. Лимурчанский разлом расположен в северной части Сихотэ-Алинской складчатой системы. Он является продолжением Центрального Сихотэ-Алинского разлома [Роганов, Васькин, 2008], смещенным по левому сдвигу на юго-запад вдоль Киселевского разлома (крайнее северо-восточное звено разлома Итунь-Илань). Обнаженность в этом районе очень плохая, и если место контакта Центрального Сихотэ-Алинского разлома с Киселевским более или менее определяется, то для Лимурчанского непосредственные полевые наблюдения сделать этого не позволяют. Обработка ЦМР расчетом модуля градиента рельефа (масштабный параметр t=1) (рис.2.6.1) позволяет предположить, что Лимурчанский разлом в месте причленения к Киселевскому расщепляется по меньшей мере на два (скорее, на 3) разлома. Возможно, это связано с тем, что именно это крыло испытывало абсолютное перемещение. Такой вывод позволяет уточнить геологическую карту, а также сделать определенные заключения по кайнозойской геодинамике района. 2. Текстура рельефа. На рис.2.6.2 показан пример ярко проявленной текстуры – базальтовые поля в Совгавани и районе Шкотовского плато Приморья. Хорошо выделяются лавовые потоки. 3. Кольцевые структуры. На рис.2.6.3 показана кольцевая структура, расположенная в районе города Советская Гавань. Синтезированное цветное RGB изображение получено путем расчета лапласиана поверхности Гаусса с масштабными параметрами t=62,1,142 ( составляющие R,G,B). На обычных аэрофотоснимках эта структура практически не видна.
СПИСОК ЛИТЕРАТУРЫ
Сентябрь 2014г.
| ||||||||||||||||||||||||||||||||||